Mathematical modeling in energy homeostasis, appetite control and food intake with a special attention to ghrelin (PhD thesis)

Notwithstanding considerable variations in daily food intake, animals uphold a remarkably stable body weight, since overall caloric ingestion and expenditure are exquisitely matched over long periods of time, by the process of energy homeostasis.

David E Cummings and Joost Overduin, 2007⁽¹⁵²⁾

The elegant ‘interconnected mechanisms’ by which the gastrointestinal (GI) tract regulates food intake are a marvel of biology, but the redundancy (e.g., several hormones seem to have effects in food intake)  of both GI (by means of hormones) and central nervous system (CNS, by means of satiety/satiation signals) pathways governing energy homeostasis poses formidable challenges for scientists trying to take a clear glimpse of this machinery, e.g. for designing anti-obesity and alike pharmaceuticals.

In essence, notwithstanding the astonishing advancements made over the past few decades in unscrambling many of the molecular pathways involved in energy (homeostasis) regulation, a rather cloudy understanding of “how all the pieces fit together to function as an integrated system” is what can be found for the most part in the scientific community; we discuss that in part II of the work, in a single chapter divided in several sections for numerous imperative hormones, e.g. cholecystokinin.

The current work is divided into three parts: part I is regarding fundamentals of physiology and mathematical modeling employed all over the work; part II is more generic and concerns several hormones (what we have called a “web of hormones”) and part III (divided into three chapters) is more specific, concerning a single hormone (i.e., ghrelin). The core of the work is part III, and to a certain extent part II, bearing mind we provide a literature review based on papers scattered/dispersed all over the medical science literature.

The main objective of this work is proposing a mathematical model for ghrelin dynamics (Figure 68), a model centered on the gastrointestinal tract (stomach + small intestine, a two-compartment model), with daily-like dynamics, short-term dynamics; and, simultaneously, proposing a prototype for a systems biology like model (Figure 38), a model based on numerous hormones, for understanding mathematically food intake/bodyweight control

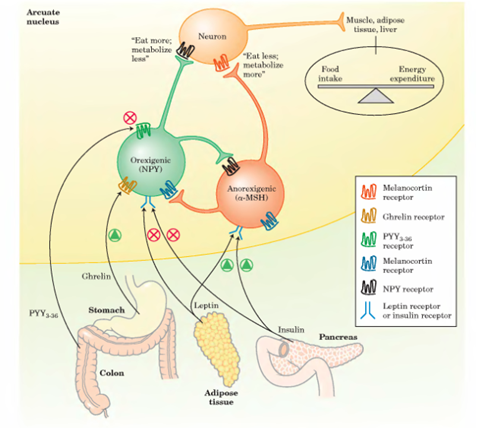
Ghrelin is a quite powerful orexigenic hormone discovered in the late 1990s that controls appetite and energy homeostasis, alongside leptin and other hormones still to be investigated in depth by the medical sciences literature. Accordingly, we provide a (simple) mathematical model, consisting of a set of ordinary differential equations detailing ghrelin dynamics combined to gastrointestinal signals due to meals. Numerical simulations are able to replicate in silico available data from the literature; additionally, we were able to fit a reduced version of the basal model to experimental data. The model is developed as a module for a bigger potential multi-compartmental structure, detailing food and energy homeostasis within a sort of "a web of hormones" (see part II and the last chapter of part III). The present contribute is to recommend a primary mathematical model for ghrelin dynamics centered in the gastrointestinal tract, with potentiality to be applied also for postabsorptive states, left mainly as future works. We go on with the model by presenting mainly two variations, further unfolding is left as future endevour: tastants and stochastic version.

We test several optimization routines for the parameter estimation procedure, hybrid algorithms (global + local search), for parameter estimation, based on data published for humans (three meals a day). For all the routines, the best is a hybrid composed of simulating annealing as global search and pattern search as local search. In the objective function (sum of the squared errors, SSE), we apply artificial neural networks (a two-layer feedforward neural network) for generating new data from the data already published, a strategy adopted to increase the data set. In the last part of the chapter about ghrelin modeling (part III), we propose several prototypes for future works based on the basal models; the model used for parameter estimation is a “minimal/reduced” model; we also provide discussions and future works for the minimal model and parameter estimation.

Key-words. Ghrelin; leptin; mathematical modelling; food intake; appetite; parameter estimation.